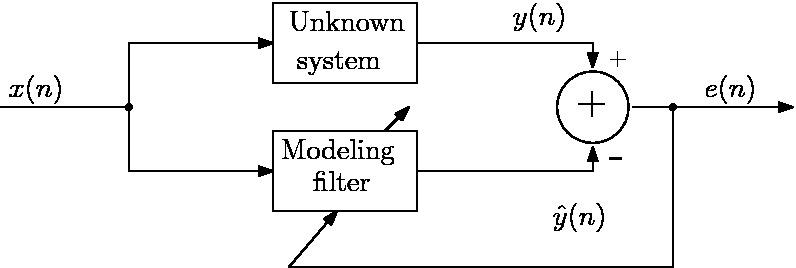
The identification and approximation of nonlinear systems is a relevant research topic in many fields of science and engineering. Since the definition of a nonlinear system is essentially based on the negation of a linearity property, there are in practice infinite kinds of nonlinear systems, Attempts have been made in the literature to define suitable sub-sets according to a given characterizing property. A model which is often used is that of the linear-in-the-parameters (LIP) nonlinear systems. A discrete-time LIP system exploits as characterizing property the linearity of the output with respect to its coefficients. The peculiarities of this class of filters are that:
i) All the filters admit, according to the time shift property, an efficient implementation based on a multichannel structure formed with linear filters;
ii) Since the coefficients appear linearly in the input-output relationship, they can be robustly estimated using the matrix methods of linear least squares;
iii) The adaptive filtering methods used for nonlinear system identification can be easily derived by those used for linear filters with favorable implications on algorithm stability and computational complexity.
The class of LIP nonlinear filters is broad and includes causal, shift-invariant, finite-memory or infinite-memory filters.
Popular nonlinear models with finite memory are truncated Volterra filters and functional link artificial neural networks (FLANN). Volterra filters exploit as basis functions the input samples and their products. As a consequence, according to the well-known Stone-Weierstrass theorem, they are universal approximators for causal, time invariant, finite-memory, continuous, nonlinear systems . However, in general, their basis functions are not orthogonal and this fact negatively affects the performance of the adaptation methods used for nonlinear system identification. On the other hand, FLANN filters usually exploit orthogonal trigonometric basis functions but are not universal approximators. The aim of this research is to find sub-classes of LIP nonlinear filters that satisfy both the above mentioned properties.
It has been already shown how it is possible to extend the definition of FLANN filters, based on sine and cosine functions, so that their basis functions become mutually orthogonal for white uniform input signals in the interval [-1, +1]. The obtained filters have been named Fourier nonlinear (FN) filters.
Then, a new family of real trigonometric functions, satisfying all the requirements of the Stone-Weierstrass theorem, has been derived. The corresponding filters have been named even mirror Fourier nonlinear (EMFN) filters, since their basis functions are even mirror symmetric, in analogy to the waveforms defining the discrete cosine transform. These basis functions are mutually orthogonal for white uniform input signals in the interval [-1, +1] and, at the same time, the EMFN filters are universal approximators.
Studies on polynomial filters, offering simultaneously the features of orthogonality and universal approximation, are currently performed resorting to Legendre polynomials.
Appropriate deterministic input signals have been proposed in the literature as an alternative to white random signals for system identification. Among them, perfect periodic sequences (PPSs) have been derived and exploited. A PPS is called perfect if all the cross-correlations between two different basis functions of the modeling filter, estimated over a period, are zero. Using PPSs as input signals, nonlinear systems can be efficiently identified with the crosscorrelation approach. Identification of a compact representation of the nonlinear system can be also easily obtained by ranking the basis functions according to their ability to reduce the MSE. Some examples of PPSs for EMFN, linear+EMFN (L+EMFN) and Legendre nonlinear filter are given at this web page.
Infinite-memory LIP nonlinear filters have also been considered in the literature since they can represent real-world systems with fewer coefficients than finite-memory counterparts. Examples include bilinear, recursive second-order Volterra (RSOV) and recursive FLANN (RFLANN) filters. Our contribution in this field is the presentation of a general theory that permits the introduction of a novel sub-class of infinite-memory LIP nonlinear filters. Within simple conditions, the recursive nonlinear system to be modeled can be approximated using a linear combination of trigonometric basis functions derived from those of the EMFN filter, using finite sets of input and past output samples. We have also proved that, according to the Stone-Weierstrass theorem, it is possible, to arbitrarily well approximate a recursive nonlinear system using such kind of recursive EMFN (REMFN) filters. Another relevant property is their bounded-input-bounded-output (BIBO) stability. It is well known that recursive filters with fixed coefficients may become unstable, according to the BIBO criterion. For example, the BIBO stability of bilinear and RSOV filters with fixed coefficients requires that the poles of their linear IIR parts be inside the unit circle of the z plane. Moreover, sufficient conditions need to be imposed on the amplitude of the input signal in order to guarantee the boundedness of the output signals. The BIBO condition is alleviated for the RFLANN filter since, as shown in our contributions, no additional constraints on the boundedness of the input signal are needed. Finally, in the case of the REMFN filter, no conditions at all need to be checked, since this filter is always BIBO stable.
The research is done in cooperation with the Department of Basic Sciences and Foundations, University of Urbino, Italy.

